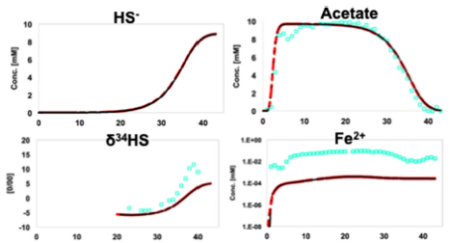
Simulated and observed trends of aqueous species comparing agreement between models. Circles show observed data, while lines show simulated trends (CrunchFlow: red, Toughreact: black)
A benchmark problem set was developed for the simulation of kinetic sulfur isotope fractionation that explicitly incorporates biomass growth and tests commonly-used rate law formulations for isotope fractionation.
Benchmarking studies on isotopes are fairly limited. Modelers seeking to incorporate kinetic isotope fractionation into their codes will find in this problem set a simple benchmark to verify their codes that is based on well-established reaction rate formulations and sound mass balance principles.
Summary
Despite the availability of a large number of reactive transport codes that essentially solve the same governing equations, substantial differences exist among them. Users can differentiate codes on the basis of the capabilities they offer, and the flexibility and ease of their use. For complex subsurface settings, such as those involving multiple interacting components or requiring distinct partitioning of isotopes, the only way to verify codes and build confidence is through benchmarking activities. Here, we present a benchmark problem that involves a key process in many subsurface applications, i.e. microbially mediated sulfate reduction. This benchmark problem involves a well-characterized system where multiple aqueous species exist in tandem, Fe and S cycling are intricately coupled, and require distinct partitioning of sulfur isotopes. To ensure that the results presented in this paper were the correct solutions to the problems posed, the general-purpose reactive transport codes CrunchFlow, ToughReact, PHREEQC and PHT3D were used to perform the simulations, showing excellent agreement. Overall, this study presents a benchmark to users to assess differences (or similarities) across codes based on capabilities for kinetic isotope fractionation, biomass growth, and different rate law formulations.
Citation
Y. Cheng, B. Arora, S. S. Şengör, J. L. Druhan, C. Wanner, B. M. van Breukelen, and C. I. Steefel, “ Microbially mediated kinetic sulfur isotope fractionation: reactive transport modeling benchmark.” Comput Geosci. (2020). [DOI: 10.1007/s10596-020-09988-9]