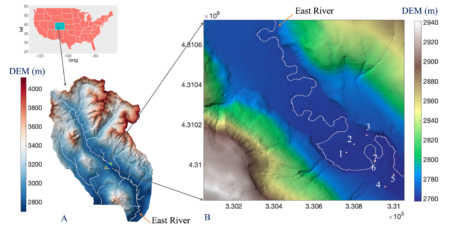
We develop an approach for estimating missing groundwater data at a study site located in the East River watershed, a high-elevation catchment in southwestern Colorado (a). Seven monitoring wells (WLE1 to WLE7, marked as 1 to 7) are located in the East River watershed floodplain (b).
The Science
Sixty to 90 percent of the world’s water comes from alpine watersheds, but without continuous data about characteristics like groundwater levels, temperature, and precipitation it can be nearly impossible for scientists to understand groundwater dynamics well enough to help predict the amount or quality of water coming from those mountains. Machine learning (ML)–using computer science to make predictions and inferences about data–can be used to help estimate missing data due to power outages, failures in the equipment used to gather the data, and extreme weather events from previous datasets gathered on these features. Researchers recently evaluated several ML-based techniques to infer data missing from datasets previously obtained at multiple wells in the East River Watershed located in southwestern Colorado. The team developed a new sequential approach to use existing data from previous time periods to estimate the missing extremes of a hydrograph, which shows the rate of water flow over time. This approach allows for missing groundwater data in the East River to be estimated with high accuracy.
The Impact
Environmental datasets such as groundwater data are often incomplete and contain missing entries due to various reasons such as adverse weather conditions or delays in collecting sensor data. Scientists rely on data about previous groundwater levels to predict the availability, quality, and function of freshwater. However, without continuous data sets, it is challenging to use scientific models that require this data to properly predict groundwater functioning. Researchers showed that ML techniques could be used to fill in gaps in these data series using previous data from a single well or data from surrounding wells. Overall, this new approach can be transferable to gap-fill other environmental datasets like precipitation and soil moisture. Complete groundwater and other environmental data are critical to monitor how freshwater and other natural resources may change as climate and environmental conditions change.
Summary
It is not uncommon for groundwater data series to have missing records due to factors like malfunctioning technology and physical disturbances. Researchers explored several techniques to gap-fill groundwater datasets, focusing on missing data patterns that are either random, such as data missing from one day in a series of several days, or contiguous gaps, such as a lack of data for an entire month during an observed time period. The researchers considered data from both single and multiple wells, looking to gap-fill missing groundwater entries in a well using that same well’s time-series data in the case of single wells, and for multiple wells using available data from neighboring wells to gap-fill a specific well’s missing groundwater data. They compared three machine-learning methods to understand which was better at estimating missing data for either the random or contiguous patterns. All three were shown to estimate up to 90% of random gaps in the groundwater time series over a two-year period. Multiple-well methods could effectively estimate up to 50% of missing contiguous gaps, but failed to capture extremes for the same period. The research team has developed an effective strategy to capture missing extremes in the groundwater time series and demonstrated its application across multiple wells in the Colorado East River floodplain.
Citation
Dwivedi, D., Mital, U., Faybishenko, B., Dafflon, B., Varadharajan, C., Agarwal, D., Williams, K H., Steefel, C. I. and Hubbard, S. S. Imputation of Contiguous Gaps and Extremes of Subhourly Groundwater Time Series Using Random Forests, Journal of Machine Learning for Modeling and Computing, Volume 3, 2022, Issue 2, DOI: 10.1615/JMachLearnModelComput.2021038774